Intro to Part 3

In part 3, we’ll be using our new javascript word vector model to create a service that lists words similar to an input word.

Finding similar words

If we’re given a word, we want to find words similar to it. How do we do that? The most fundamental measure of distance is the euclidean distance, however; it’s not used often in machine learning applications. What makes sense to our intuitions tuned for 2d and 3d spaces might not work in a 300d space (see: 1 2 3 4).

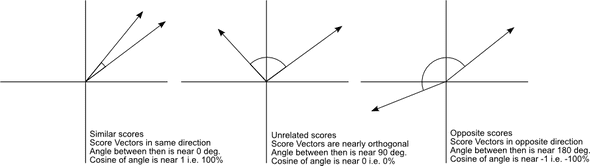
Instead, we can use cosine similarity, which will tell us if vectors are roughly pointing in the same direction or not:

Calculating cosine similarity (theory)

This dot product formula contains the cosine of the angle between two vectors:

$\mathbf{a} \cdot \mathbf{b} = || \mathbf{a} ||_2 || \mathbf{b} ||_2 \cos \theta$

Solving for $\cos \theta$, we find:

$\cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{ || \mathbf{a} ||_2 || \mathbf{b} ||_2 }$

The dot product can also be expressed as the sum of the products of the components of each vector, or:

$ \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 + \cdots + a_n b_n $

As a refresher, $ || \mathbf{a} ||_2 $ is known as the L2 norm, or euclidean norm, or magnitude of a vector.

$ || \mathbf{a} ||_2 := \sqrt{a_1^2 + a_2^2 + \cdots + a_n^2} $

A neat result is: $ || \mathbf{a} ||_2 := \sqrt{\mathbf{a} \cdot \mathbf{a}} $

Calculating cosine similarity (practice)

Now that we know

$\cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{ || \mathbf{a} ||_2 || \mathbf{b} ||_2 }$

, let’s write some javascript to calculate it.

My first stab at it was:

const dotProduct = (a, b) => {
	if (!Array.isArray(a) || !Array.isArray(b) || a.length != b.length) {
		throw 'invalid arguments';
	}
	const zippedVectors  = a.map((x, idx) => [x, b[idx]]);
	const products = zippedVectors.map(x => x[0] * x[1]);
	return products.reduce((acc, x) => acc + x, 0);
}

const magnitude = a => Math.sqrt(dotProduct(a, a));

const cosineSimilarity = (a, b) => dotProduct(a, b) / (magnitude(a) * magnitude(b));

I default to writing psuedo-immutable + functional style. However in this case, the function turned out to be much slower than it needed to be. I was able to get about a 10x speedup by not calculating the zippedVectors and products intermediate arrays:

const dotProduct = (a, b) => {
	if (!Array.isArray(a) || !Array.isArray(b) || a.length != b.length) {
		throw 'invalid arguments';
	}
	return a.reduce((acc, x, idx) => acc + (x * b[idx]), 0);
}

const magnitude = a => Math.sqrt(dotProduct(a, a));

const cosineSimilarity = (a, b) => dotProduct(a, b) / (magnitude(a) * magnitude(b));

Much better, even if the reduce is slightly awkward in my opinion.

Almost done

Now I just need a quick function to use the dotProduct function to find me a list a similar words:

export const findSimiliar = (word, threshold = 0.45, maxResults = 50) => {
	if (!(word in vectors)) { return []; }

	let results = [];
	for (let candidate of Object.keys(vectors)) {
		if (candidate == word) { continue; }

		const similarity = cosineSimilarity(vectors[word], vectors[candidate]);
		if (similarity < threshold) { continue; }

		results.push({word: candidate, similarity});
	}

	return results.sort((a, b) => b.similarity - a.similarity).slice(0, maxResults);
}

Making an API

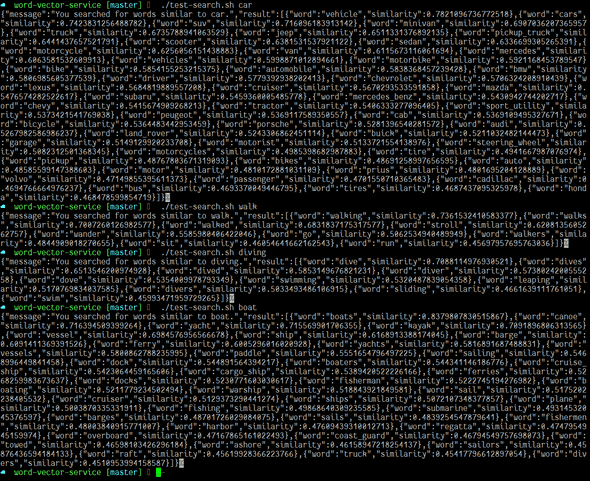
With these functions and the model, we have the guts of our API ready. I used Express & ES6 REST API Boilerplate and wrote a little bit of glue code to make an API that takes an input word and lists similar words. One important detail is I told babel not to transform my 75 megabyte model file. Here it is in action (w/ hard to read json):

Gist of above.

The code for this is on github: Code.

Up next

In part 4, we’ll add the service to our react app.